Дневник крипто-трейдера.
-
500+подписчиков
-
ПопулярностьТоп-78
-
Постов1,934
-
Просмотров379,240
-
Подписок564
-
Карма автора+13,452
-
elterion, Отвечу на твой вопрос, хоть ты спрашивал и не у меня. За 6 лет трейдинга я при
+101
-
Расскажу полную историю о моём опыте торговли в форекс-брокере, который не хотел выводить мне деньги
+76
-
Так заплюсовали пост с просьбами рефок. Я в шоке, если честно. Долгое время, рефки кидать зазорным с
+75
-
Galax, пиши сразу названия таких бирж. Может, спасёшь этим кому-нибудь деньги.
+42
-
Я называю это "возвратом". Люди начинают учить других, когда чего-то добились, потому что делать пол
+39
-
-
Galax @ 23.07.25
Во-первых, понятно, что каждый день нужно брать одну и ту же фракцию банкролла обозначим ее f.
Ср.геометрическое будет:
(1 + f * 1) * (1 - f * 0.6)
И вот нужно подобрать при каком f это ср.-геометрическое будет наибольшим.
Подставляем f = 0.3333 (из формули Келли) и получим:
(1 + 0,33 * 1) * (1 - 0,33 * 0,6) = 1,0666.
Не понял. Т.е. ты вкладываешь f-банкролла, а получаешь 1=100%, что больше f. Наверно ты должен получить f.
Вкладываешь в ставку 1 копейку, а получаешь с 50% - миллиард?
-
Jak @ 24.07.25
Galax @ 23.07.25Во-первых, понятно, что каждый день нужно брать одну и ту же фракцию банкролла обозначим ее f.
Ср.геометрическое будет:
(1 + f * 1) * (1 - f * 0.6)
И вот нужно подобрать при каком f это ср.-геометрическое будет наибольшим.
Подставляем f = 0.3333 (из формули Келли) и получим:
(1 + 0,33 * 1) * (1 - 0,33 * 0,6) = 1,0666.
Не понял. Т.е. ты вкладываешь f-банкролла, а получаешь 1=100%, что больше f. Наверно ты должен получить f.
Вкладываешь в ставку 1 копейку, а получаешь с 50% - миллиард?
Тут нужно не запутаться, когда переходим от процентов к дробным числам.
1 - это 100%, 0,6 - это 60%
В оригинальной задаче (без балансировки) будет так (f = 1):
(1 + 1*1) * (1 - 1*0.6) = 2 * 0.4 = 0.8
- при росте мы умножаем банкрол на 2 (+100%), при падении мы умножаем банкролл на 0,4(-60%)
Если f = 0.33, то будет так:
(1 + 0,3333 * 1) * (1 - 0,3333 *0,6) = 1,3333 * 0,8 = 1,0666
- при росте мы умножаем банкролл на 1,3333 (+33%), при падении мы умножаем банкролл на 0,8 (-20%)
В результате ср.-геометрическое поднимается с 0,8 до 1,06666.
-
elterion, Проблема в том что делается сравнительно не много симулляций.
Когда у нас 2 дня, то число исходов 4 = 2^2,Когда у нас 3 дня, то число исходов 8 = 2^3,
.......
Когда у нас 1000 дней, то число исходов 2^1000 = Е+301
Чтобы получить более-менее реальную картину нужно провести сопоставимое к-во симмуляций. А это нереально.
Твои 10 000 000 - это капля в море от всех возможных вариантов.
Но для проверки критерия Келли, лостаточно будет и такого к-ва симуляций.Я тебя просил - просто подставь в код другие коеффициенты:
при росте умножаем вместо 2 на 1,33, а при падении умножаем вместо 0.4 на 0,8.
Ну или переведи в свои метрики, если у тебя код по другому устроен.
-
mandeljambes, Спасибо, посмотрю твою ссылку.
Ексель посмотрел, там всего 100 симуляций. Это совершенно мало.Вот человек делает в коде по 10 000 000 симуляций - и даже это капля в море.
-
HuanXIV @ 22.07.25
Чуточку видоизменим игру.
С вероятностью 99 процентов ты удваиваешься, с вероятностью 1 процент ты теряешь все.
Матожидание = 0.99 * 100 - 0.01*100 = плюс 98 процентов.
Тем не менее вряд ли кто-то согласиться инвестировать на таких условиях не то , что 10 000 лет, но даже 10 лет
Будь аккуратней с формулировками. Ведь если нигде не было оговорено, что нужно всегда ставить весь банкролл, то игра будет очень плюсовой (мы уже знаем критерий Келли).
И на форуме могут найтись люди, любители подловить на формулировках, и поспорить с тобой.
-
Закрыл сделку по эфиру:
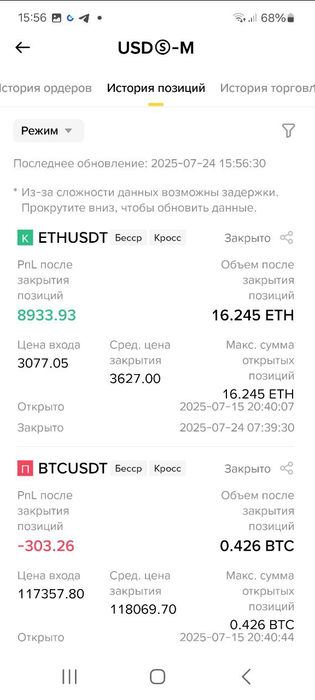
Итого вышло +8,6К дохода.
На пике было +11К плавающего дохода.
Почему закрыл?
Не спрашивайте, я не смогу ответить.
Просто утром проснулся, посмотрел на график и решил зафиксировать профит.
Это всегда сложное решение - когда фиксировать профит, а когда терпеливо ждать окончания коррекции.
Началась коррекция на часовом тайм-фрейме и я решил посидеть в сторонке.
Я намереваюсь, когда эта коррекция закончится и рост возобновится, попробовать снова войти в лонг.
Надеюсь, что цена перезахода будет не хуже цены выхода.
Но часто бывает наоборот.
И да, обнаружил, что на фьючерсах есть пара ETHBTCUSDT - то что я пытался синтезировать с помощью двух позиций.
А можно было просто открыть лонг по этой паре.
-
Посмотри в сторону опционов. Они дадут тебе возможность заработать денег пока ты ждёшь отката.
-
Вижу особо никому не интересно читать эти сухие математические формулы.
Но хочу закончить эту тему. Некоторые ребята потратили свое время и я решил тоже немного потратить.
Так как Монте-Карло не может дать полной картины, я попробовал сделать это на Excel с помощью формул.Вот мой файл Excel:
Формула_Келли.xlsx (28.3 килобайт)Тут сравниваются две стратегии - одна при полной загрузке банкролла (f=1) и вторая, при ребалансировке по 0.3333 банкролла (f = 0.3333). Рассчеты сделаны для 100 дней (для большего к-ва слишком муторно делать).
Методология расчета такая (это может пригодится при решении любых подобных задач):
Для 100 дней пишем в одну колонку сколько есть дней роста, а в другую - сколько дней падения (100 - дней роста).
У нас получится 101 вариант от 100 - 0, 99 - 1, ..., до 0-100.
Считаем вероятность такого распределения по формуле БИНОМРАСП в Excel.
Например распределение 50-50 имеет вероятность 0,0795 (7,95%), 60-40 (1,08%), а 100-0 Е-31.
В следующей колонке считаем какой вклад дадут дни роста - это рост за один день возводится в степень -ква дней роста.При f= 0.33 множитель будет 1.33 его возводим в степень (например 60 при распределении 60-40).
В следующей колонке делаем аналогично для дней падения - при f = 0.33 возводим 0,80 в степень 40 (при распределении 60-40).
Далее эти две колонки перемножаются между собой - получается реальный результат какой мы получим банкролл при распределении 60-40 (и всех остальных).
Таким образом мы имеем полный расклад - для каждого распределения от 100-0 до 0-100 мы имеем вероятность такого исхода и какой результат будет при таком распределении.
Что интересного можно узнать из этой Excel таблицы.
Для варианта без ребалансировки:
Результат больше 1 получается при распределении 57-43, все что хуже этого распределения это минусовый результат.
Вероятность такого события 86%. Т.е. с вероятностью 86% у нас будет минусовый результат.
И это всего для 100 дней. Для 1000 и тем более для 10 000 все будет намного хуже.
Для варианта с ребалансировкой при f = 0.33:
Результат больше 1 будет при распределении 44 - 56 - только в 10% случаев будет минусовый результат.
Если сравнить две стратегии между собой:
первая стратегия (без балансировки) побеждает вторую только начиная с распределения 64 - 36. Все что ниже 64-36 стратегия с ребалансировкой побеждает.
Вероятность этого больше 99%.
Итого: вторая стратегия побеждает первую в 99% случаев.
Для 1000 и 10 000 дней все будет еще хуже.
-
Итак хочу подвести кое-какие итоги.
Я предлагаю вам выбрать одну из стратегий на 10000 дней (на 30 лет).
Одна с ребалансировкой, вторая - без.
Но я должен вам честно описать возможные расклады.
В первой стратегии вы с вероятностью больше 99% заработаете все деньги мира, а с вероятностью близкой к нулю потеряете вложения (1$).Во второй стратегии ваше ЕВ намного больше, чем в первой (на много порядков), но расклад такой:
с вероятностью близкой к 100% вы потеряете свои деньги, но с вероятностью близкой к нулю заработаете намного больше чем в первой стратегии (т.е. все деньги мира еще надо умножить на много-много раз).
Напоминаем, что этот выбор делается один раз в жизни, у вас не будет больше вариантов прожить жизнь еще раз (или миллионы раз).
Так какую стратегию вы выберете? -
Galax @ 23.07.25
Т.е. проведи симуляцию как ты делал раньше на полный банкролл, но сейчас сделай при 30%, 33%, 35%.
И посчитай среднюю доходность для каждого из трех вариантов.
Если все верно, то случай при 33% должен давать большую доходность, чем два соседних варианта для 30% и 35%.
Также интересно бы было узнать, какой процент симмуляций будет в минусе (т.е. на выходе банкролл меньше, чем на входе).
Результаты:
Количество симуляций: 10_000_000
Процент от банкролла: 25%
Прибыльных симуляций: 9_999_997 (100.000%)
Убыточных симуляций: 3 (0.000%)
Средний доход за 1_000 дней: 2.1227149037338208e+20
Процент от банкролла: 30%
Прибыльных симуляций: 9_999_942 (99.999%)
Убыточных симуляций: 58 (0.001%)
Средний доход за 1_000 дней: 1.9554286665824935e+24
Процент от банкролла: 33%
Прибыльных симуляций: 9_999_700 (99.997%)
Убыточных симуляций: 300 (0.003%)
Средний доход за 1_000 дней: 2.783991419969801e+27
Процент от банкролла: 35%
Прибыльных симуляций: 9_999_386 (99.994%)
Убыточных симуляций: 614 (0.006%)
Средний доход за 1_000 дней: 3.7326711877690065e+26
Процент от банкролла: 40%
Прибыльных симуляций: 9_992_919 (99.929%)
Убыточных симуляций: 7_081 (0.071%)
Средний доход за 1_000 дней: 9.254492998291453e+28
Процент от банкролла: 50%
Прибыльных симуляций: 9_801_829 (98.018%)
Убыточных симуляций: 198_171 (1.982%)
Средний доход за 1_000 дней: 3.2322339489468303e+30
Процент от банкролла: 60%
Прибыльных симуляций: 7_852_305 (78.523%)
Убыточных симуляций: 2_147_695 (21.477%)
Средний доход за 1_000 дней: 6.73562883675269e+31
Процент от банкролла: 70%
Прибыльных симуляций: 3_403_708 (34.037%)
Убыточных симуляций: 6_596_292 (65.963%)
Средний доход за 1_000 дней: 2.055881067935218e+29
Процент от банкролла: 100%
Прибыльных симуляций: 47 (0.000%)
Убыточных симуляций: 9_999_953 (100.000%)
Средний доход за 1_000 дней: 743.3435015477849
Не очень понимаю, как это поможет проверить критерий Келли, ведь ЕВ (если считать через среднее арифметическое) с ростом доли от банкролла растёт, как ему и положено. Хотя при таком количестве симуляций модель не очень стабильна даже при низких значениях доли банкролла, а с ростом этой доли количество убыточных прогонов начинает стремительно расти и результат прогона в ЕВ становится вообще не репрезентативным.
Так какую стратегию вы выберете?
Очевидно ту, которая с ребалансировкой. Нафига мне "все деньги мира умноженные на много-много раз"? Я не жадный, мне просто всех денег мира с вероятностью 99.997% за глаза хватит.
Сообщение отредактировал elterion - 24.7.2025, 22:21 -
elterion, Спасибо, что потратил свое время.
Хотя к-во симуляций не очень большое для такого к-ва дней (1000), но результат в принципе прогнозируемый.
Распределения, которые не попали в твои симуляции, они случаются реже чем 1 / 10 000 000.
А за чем расчитывать на такие редкие события, когда у нас всего один шанс сыграть в эту игру?
И этот один шанс будет быстрее один из твоих 10 000 000, чем тот который не попал в твои симуляции.
И даже на 10 000 000 симуляций видно, что при 100% банкролла мы почти всегда банкроты, а при ребалансировке по 0.33 мы почти с 100% вероятностью зарабатываем деньги порядка Е+27.
elterion @ 24.07.25
Очевидно ту, которая с ребалансировкой. Нафига мне "все деньги мира умноженные на много-много раз"? Я не жадный, мне просто всех денег мира с вероятностью 99.997% за глаза хватит.
Вроде очевидный выбор, но тем не менее на форуме время от времени возникают споры на подобную тему (я застал минимум два таких спора). Я уже не помню деталей того спора, может кто-то дать ссылку на спор с Ritsar?
Этим примером я хотел показать, что не всегда нужно гнаться за максимальным ЕВ. Нужно еще учитывать риски.
И иногда нужно сознательно понижать ЕВ, если таким образом убираются риски. Именно это и позволяет сделать ребалансировка.
Этот пример выбран из-за того, что при таких процентах (+100% и -60%) этот эффект ребалансировки максимально виден.
Т.е. среднее-арифметическое выше 1 (EV положительное), а ср.-геометрическое ниже 1 (стоимость акции на дистанции стремится к нулю). Чем больше к-во дней для инвестиций, тем больше выражен этот эффект (когда стратегия с ребалансировкой побеждает стратегию без ребалансировки).
Но даже если эти вероятности роста и падения, не такие экстремальные, то все равно ребалансировка имеет тот же эффект. Просто она не будет так заметна и не так очевидна.
Все равно ср.геометрическое покажет более ожидаемый на практике результат инвестиций, чем ср.-арифметическое. Поэтому в трейдинге и ориентируются на ср. геометрическое.
Еще в видео о Формуле Келли прозвучала фраза про эргодичность. Я такое слово и не слышал раньше, нужно будет погуглить, что это такое и как оно относится к нашей теме.
-
Galax, Вот тебе еще на тему
A casino offers a game of chance for a single player in which a fair coin is tossed at each stage. The initial stake begins at 2 dollars and is doubled every time tails appears. The first time heads appears, the game ends and the player wins whatever is the current stake. Thus the player wins 2 dollars if heads appears on the first toss, 4 dollars if tails appears on the first toss and heads on the second, 8 dollars if tails appears on the first two tosses and heads on the third, and so on.
What would be a fair price to pay the casino for entering the game?
Сколько бы ты заплатил за участие в игре с бесконечным +ЕВ?
-
-
-
Nameless00 @ 24.07.25
Кто-нибудь знает как с айфона удалить вот ту фигню что выше? Ткнуть в нее как следует не получается, кнопка удалить не работает.
Galax @ 24.07.25
Я не очень понял в чем подвох?
Я же не проигрываю деньги никогда. Или я должен отдельно что-то заплатить, чтобы начать играть с двух долларов?
Да, почём, максимум, ты был бы готов купить право участия в такой игре?
-
Казино предлагает азартную игру для одного игрока, в которой на каждом этапе подбрасывается монета. Начальная ставка составляет 2 доллара и удваивается каждый раз, когда выпадает решка. Когда выпадает орёл в первый раз, игра заканчивается, и игрок выигрывает сумму, равную текущей ставке. Таким образом, игрок выигрывает 2 доллара, если выпадает орёл при первом подбрасывании, 4 доллара, если решка выпадает при первом подбрасывании и орёл при втором, 8 долларов, если решка выпадает при первых двух подбрасываниях и орёл при третьем, и так далее. Какую справедливую цену казино следует заплатить за участие в игре?
Перевел для вас.
-
ЕВ игры стремится к $2 (2/2+1/2+0,5/2...)
Но выиграть можно все деньги мира (хоть и с исчезающе малой вероятностью).
Думаю, справедливая цена такой игры для казино должна равняться баксам трем-пяти в зависимости от собственного капитала. Не двум, т.к. зачем казино качать диспу с нулевым ев.
В любом случае это не решается чисто математически.
-
Mercator @ 25.07.25
ЕВ игры стремится к $2 (2/2+1/2+0,5/2...)
Ты ЕВ неправильно посчитал.
Mercator @ 25.07.25
В любом случае это не решается чисто математически.
Ну почему же? Всё уже
украденорешено до нас... -
k7scooter @ 24.07.25
Посмотри в сторону опционов. Они дадут тебе возможность заработать денег пока ты ждёшь отката.
Извини, что сразу не отвечаю - не хватает времени на все стороны отвечать.
Ты имеешь ввиду ту стратегию, что ты раньше описал - 7%-8% АПР на покупке биткоина и его шорте?
Для крипты 7-8% АПР это очень мало.
Простой стейкинг USDT часто дает такой АПР. Но его преимущество в том, что деньги можно в любой момент закинуть и в любой момент забрать. Награды засчитываются каждый час и ввод-вывод не стоит никакой комиссии.
Так что когда у меня простаивают какие-то средства, то я их закидываю в Simple Earn. А когда подвернется, что-то более выгодное, то я безболезненно забираю эти средства из стейкинга.
Также довольно легко иметь 10% АПР на фандинге биткоина.
Большую часть времени фандинг биткоина стоит 0.01% (последние два месяца вообще не меняется).
Это означает, что каждые 8 часов вы получаете за шортовую позицию 0,01%.
Переводим это в АПР: 0,01 * 3 *365 = 11% АПР.
Т.е. мы можем купить 1 BTC на споте и одновременно открыть шорт на 1 BTC на фьючерсах и получать довольно длительное время 11% АПР.
Но не забываем о комиссии - она 0.10% на споте и 0.02% на фьючерсах.
За вход в хеджированную позицию вы заплатите 0.12% и столько же за выход - итого 0,24% (это я еще не учитываю спред и возможные проскальзывания).
А за фандинг получаем 0,01 за 8 часов, или 0,03 за сутки.
Выходит чтобы покрыть комиссии нужно 8 суток. Т.е. первые 8 суток такой хеджированной позиции будут только отбивать комиссии и только затем будет идти профит.
Так что такой фандинг выгодный только тем, кто морозит средства в нем на длительный срок (месяц и больше).
Нет гибкости - я не могу в любой момент забрать средства из-за дорогих комиссий.
Твоя стратегия с опционами наверное имеет такие же комиссионые затраты и поэтому тоже выгодна только на длительный срок. Но мне проще работать с фьючерсами, чем с опционами. Средства на кросс-марже могут служить обеспечением и для других сделок.
Правда время от времени фандинг растет. В прошлом году на эйфории роста битка фандинг поднимался до 0.09% - а это уже 90% АПР. Такой фандинг уже выгодно зарабатывать - нужно только одни сутки чтобы отбить комиссии, а дальше чистый неплохой доход в 90% АПР.
Так что 10% АПР для крипты это мало. Если у тебя есть более профитные варианты, то давай предлагай.
- Вы сможете оставлять комментарии, оценивать посты, участвовать в дискуссиях и повышать свой уровень игры.
- Если вы предпочитаете четырехцветную колоду и хотите отключить анимацию аватаров, эти возможности будут в настройках профиля.
- Вам станут доступны закладки, бекинг и другие удобные инструменты сайта.
- На каждой странице будет видно, где появились новые посты и комментарии.
- Если вы зарегистрированы в покер-румах через GipsyTeam, вы получите статистику рейка, бонусные очки для покупок в магазине, эксклюзивные акции и расширенную поддержку.


Galax, я потыкал в свою модельку, но результаты получаются очень не стабильными (я сейчас про изначальную постановку задачи, только количество дней уменьшил до 1_000) - даже при 10_000_000 итераций в одном прогоне может быть 1 плюсовая траектория, которая приносит всего x50 от начального капитала, а в следующем - таких траекторий может быть 60 и доход от них измеряется числом в 8 степени. У нас дисперсия растёт экспоненциально с увеличением числа дней, так что я не уверен, что моделирование методом Монте-Карло когда-нибудь сойдётся... А стало быть доверять такому моделированию я бы поостерёгся.
А насчёт формулы Келли - а как она может "не работать", если это просто решение диффура в общем виде? С ней другая проблема - нам необходимо точно знать истинную вероятность события, потому что даже небольшая погрешность в определении вероятности сильно влияет на результат.