Полублефы. Помогите разобраться с математикой Полублефов
-
ПопулярностьТоп-4911
-
Постов56
-
Просмотров2,245
-
Подписок1
-
Карма автора+5
-
В той модели, формулу которой я привёл, мы даже не даём оппу возможности рейза. Если дать, то это уж
+1
-
Необходимая частота фолда для рук с нулевым эквити находится по формуле - риск / (риск + вознагражде
+1
-
Valmiki, А не подскажите формулу исходя из тех которые Вы приводили ранее?)Ну чтобы можно было
0
-
Elijah96, что-то можно, что-то не очень - только это всё не очень практично
0
-
Valmiki, У меня тут еще вопрос появился)А можно ли как-то либо мои либо Вашу либо какую другую
0
-
-
Здравствуй)
По моему мы с Вами уже решали проблему с ФЭ и поэтому попытаюсь помочь и в этом вопросе)
Вообще(как ни странно)в покере можно выиграть либо блефом,либо на шоудауне с натсом
Поэтому нужно рассчитать ЕВ и по блефу и ЕВ по эквити,а после подставить эти значения в формулу матожидания
Возьмем Ваш же пример
Fawn @ 21.02.25
Пример:
Мы хотим поставить пот-бет (100% пота) против оппа, который фолдит на пот-бет РОВНО 40% рук.
Точка безубыточности при ставке в 100% банка = 50%. (Т.е. если опп будет фолдить более 50% рук из своего диапа - ставка в пот будет приносить незначительную автоприбыль.)
Предположим что пот равен 100
Хиро делает пот-бет(100)
Опп размышляет.....
Далее возможны две ситуации,по блефу и по эквити:
1)Опп сбрасывает в 40 процентах случаев и мы выигрываем(блеф)
2)Опп коллирует и мы выигрываем в ИКС процентах случаев и проигрываем в ИКС процентах случаев(эквити)
Но как найти эти ИКС?
В этом может помочь формула матожидания
Рассчитаем первую ситуацию(ЕВ по блефу):
Опп сбрасывает и мы выигрываем пот в 40 процентах случаев
100*40%=40
В случае фолда оппа вероятность проигрыша очевидно равна нулю,и тогда матожидание проигрыша от фолда тоже равно нулю(матожидание проигрыша от фолда в формулу писать не будем,так как это ноль)
Рассчитаем вторую ситуацию(ЕВ по эквити):
Опп коллит и мы выигрываем в ИКС процентах случаев и проигрываем тоже в ИКС процентах случаев
200*X%+(-100)*X%=?
Далее подставим 100*40% и 200*X%+(-100)*X% в формулу матожидания:
100*40%+200*X%+(-100)*X%
Где:
100*40% - Это матожидание выигрыша по блефу
200*X% - Это матожидание выигрыша по эквити
(-100)*X% - Это матожидание проигрыша по эквитиЧтобы найти ИКСы нужно подставить в формулу матожидания те значения,чтобы в результате получилось ноль
Ищем нужные значения для X и подставляем в нашу формулу:
100*40%+200*X%+(-100)*X%=100*40%+200*15%+(-100)*70%=40+30+(-70)=0
Где:
По блефу мы выиграем 100*40%=40
По эквити мы выигрываем 200*15%=30
По эквити мы проигрываем (-100)*70%=-70
То есть если у Оппа ФЭ равно 40 процентов,то эквити руки должно быть 15 процентов,чтобы в матожидание было равно нулю
Пояснение:
Если Хиро выигрывает то он выигрывает пот(100) и ставку оппа(100),получается 200
А если хиро проигрывает,то проигрывает только собственную ставку(100)
Fawn @ 21.02.25
Как рассчитать, сколько минимально эквити должна иметь рука, чтобы ставить с ней на полублефе при РАЗНОМ количестве ФЭ?
ФЭ и эквити руки тесно связанны
Чем больше ФЭ тем меньше может быть эквити руки,и наоборот,чем меньше ФЭ тем больше должно быть эквити руки
Ведь чтобы была прибыль,пот нужно выигрывать больше чем в 50% случаев(таково уж матожидание)(в случае для двух игроков)
Поэтому чтобы ставить с рукой на полублефе при разном ФЭ,можно рассчитать эквити руки а затем найти диапазон ФЭ(минимальное и максимальное значение),при котором с этой рукой можно блефовать
Сообщение отредактировал Elijah96 - 21.2.2025, 22:03 -
В первом посте расчеты не верны)
Тут все верно(исправил)
Предположим что пот равен 100Хиро делает пот-бет(100)
Опп размышляет.....
Далее возможны две ситуации,по блефу и по эквити:
1)Опп сбрасывает в 40 процентах случаев и Хиро выигрывает(блеф)
2)Опп коллирует и Хиро выигрывает в ИКС процентах случаев и проигрыват в ИКС процентах случаев(эквити)
Но как найти эти ИКС?
В этом может помочь формула матожидания
Рассчитаем первую ситуацию(ЕВ по блефу):
Опп сбрасывает и Хиро выигрывает в 40 процентах случаев
100*40%=40
В случае фолда Оппа,вероятность проигрыша Хиро очевидно равна нулю,и тогда матожидание проигрыша тоже равно нулю(матожидание проигрыша в формулу писать не будем,так как это ноль)
Рассчитаем вторую ситуацию(ЕВ по эквити):
Опп коллит и Хиро выигрывает в ИКС процентах случаев и проигрывает тоже в ИКС процентах случаев
200*X%+(-100)*X%=?
Далее подставим 100*40% и 200*X%+(-100)*X% в формулу матожидания:
100*40%+200*X%+(-100)*X%
Где:
100*40% - Это матожидание выигрыша по блефу
200*X% - Это матожидание выигрыша по эквити
(-100)*X% - Это матожидание проигрыша по эквитиЧтобы найти ИКСы нужно подставить в формулу матожидания те значения,чтобы в результате получился ноль
Ищем нужные значения для X и подставляем в нашу формулу:
100*40%+200*X%+(-100)*X%=100*40%+200*20%+(-100)*80%=40+40+(-80)=0
Где:
По блефу Хиро выигрывает 100*40%=40
По эквити Хиро выигрывает 200*20%=40
По эквити Хиро проигрывает (-100)*80%=-80
То есть если у Оппа ФЭ равно 40 процентов,то эквити руки Хиро должно быть 20 процентов,чтобы его матожидание было равно нулю
Пояснение:
Если Опп колл и Хиро выигрывает,то он выигрывает пот(100) и колл Оппа(100),получается 200
Если Опп фолд то Хиро выигрывает только пот(100)
Если Опп колл и Хиро проигрывает,то Хиро проигрывает только собственную ставку(100)Сообщение отредактировал Elijah96 - 21.2.2025, 23:06 -
Elijah96, Привет!
Elijah96 @ 21.02.25
По моему мы с Вами уже решали проблему с ФЭ и поэтому попытаюсь помочь и в этом вопросе)
Да, я помню) Спасибо большое за помощь в прошлый раз!
Elijah96 @ 21.02.25
Далее подставим 100*40% и 200*X%+(-100)*X% в формулу матожидания:
100*40%+200*X%+(-100)*X%
Где:
100*40% - Это матожидание выигрыша по блефу
200*X% - Это матожидание выигрыша по эквити
(-100)*X% - Это матожидание проигрыша по эквитиНебольшая поправка:
Т.к. мы используем переменную "X" в одной формуле - она не может быть разных значений. Я имею в виду, что мы не можем утверждать, что Х = 30% и в этой же формуле Х = 70%.
Плюс к этому, суммарное [ "% Эквити на выигрыш" + "% Случаев на проигрыш" ] - эта сумма всегда должна равняться 100% (т.к. если мы выигрываем, например в 1% случаев, то проигрываем в 99% случаев и наоборот).
Поэтому, предлагаю немного скорректировать формулу и вместо двух одинаковых "Х", использовать где [эквити на выигрыш] = [ "Х%" ], а где [ эквити на проигрыш ] = [ "100% - Х%" ].Ну, в этом духе) Чтобы вторая переменная просто зависела от первой. Плюс, так даже удобнее. Никогда не будет путаницы, как в первых расчётах.
Надеюсь, более-менее понятно объяснил)Спасибо большое за формулу мат. ожидания! Никогда не пользовался ей и особо не видел, чтобы применяли.
Вроде бы всё понятно. Хотелось бы вывести более простую формулу, чтобы просто подставлять "Требуемое ФЭ" куда надо и бет-сайзинг и получать готовый ответ.Попробую такую формулу вывести самостоятельно.В остальном - вы полностью решили мою проблему, ещё раз спасибо большое!P.s. Если выведу более удобную формулу - отпишу сюда.Сообщение отредактировал Fawn - 22.2.2025, 0:19 -
Elijah96, решил проверить формулу с помощью другой формулы и...
О нет! Всё сломалось! 😭
Есть такое понятие, как точка безубыточности блефа.
Что это значит? Это значит, что если мы ставим ставку в 1/2 пота и у нас 0% эквити - ставка будет нулёвой, при условии, что опп фолдит 33%.
Значит, в нашей формуле, если опп фолдит на ставку 1/2 пота ровно 33% рук - должен получиться ноль.
Проверим:
Для примера возьмём ситуацию, где мы ставим 50бб в банк 100бб на ривере и у нас 0% эквити.
Немного модифицировал изначальную формулу Elijah96, для удобства:
[ Размер пота*Реальное ФЕ% ] + [ (размер пота ДО ставки + размер ставки) * X% ] + [ (-1 * размер ставки) * (100% - Х%) ]
Подставляем значения:
[ 100 * 33% ] + [ (100 + 50) * 0% ] + [ ( -1 * 50 ) * (100% - 0%) ] = 33 -50 = -17
Получается отрицательное значение! А должен быть ноль((
Что-то не сходится.
-
-
Тут ОЧЕНЬ важный момент
Какой процент Хиро вложил в пот относительно самого пота
Если играют два игрока то в пот они могут вложить 50% на 50%
Если играют три игрока то в пот они вкладывают по 33%
Если играют четыре игрока то в пот они вкладывают по 25%
И так далее
Fawn @ 21.02.25
Для примера возьмём ситуацию, где мы ставим 50бб в банк 100бб на ривере и у нас 0% эквити.
Если в этом примере играют два игрока и они сформировали банк 100бб еще на префлопе а далее флоп-терн чек-чек и на ривере Хиро делает ставку в 50бб в пот 100бб
То Хиро вложил в пот 50бб еще на префлопе и 50бб на ривере
А Опп вложил пока только 50бб на префлопе
А дальше пример в предыдущем обсуждении
-
И еще момент
Elijah96 @ 21.02.25
Чем больше ФЭ тем меньше может быть эквити руки,и наоборот,чем меньше ФЭ тем больше должно быть эквити руки
Ведь чтобы была прибыль,пот нужно выигрывать больше чем в 50% случаев(таково уж матожидание)(в случае для двух игроков)
В Вашем примере
Fawn @ 21.02.25
Для примера возьмём ситуацию, где мы ставим 50бб в банк 100бб на ривере и у нас 0% эквити.
Эквити руки 0,а значит выиграть можно только блефом в 33% случаев
Поэтому по формуле и получается -17,и нуля там быть не может
То есть чтобы ЕВ было нулевое,то выигрывать нужно в 50% случаев
А мы выигрываем лишь в 33%
Отсюда и отрицательное ожидание
Ситуация изначально проигрышная
-
при потбете с 40% ФЭ нужно ~11% эквити
формула в данном случае 2-3eq/1-3eq=1/fe
-
Необходимая частота фолда для рук с нулевым эквити находится по формуле - риск / (риск + вознаграждение)
То есть, например, ставка 10 bb - это риск, пот 10 bb - вознаграждение, получается 10 / (10 + 10) = 50%
Если приравнять пот к единице, то эту формулу можно выразить как bet / (bet + 1), где bet - размер ставкиЕсли мы говорим про руки, у которых есть некоторое эквити, то формула примет следующий вид - (риск - eq * (2 * риск + вознаграждение)) / (риск - eq * (2 * риск + вознаграждение) + вознаграждение). Её можно записать и так - (bet - eq * (2 * bet + 1)) / (bet - eq * (2 * bet + 1) + 1)
Это может казаться запутанным, но на самом деле не особо. Это всё та же первая формула просто из числителя и знаменателя отнимается - eq * (2 * риск + вознаграждение), то есть пот, который образуется после колла ставки, помноженный на эквити. Для нашего примера это - eq * 30. Почему это вычитается? Простое объяснение - тот, кто ставит с полублефом на самом деле вот этой величиной eq * 30 не рискует, это его законная доля пота, которая ему принадлежит по эквити, поэтому он должен вычесть её из риска изначальной формулы - из числителя и знаменателя. Если по сложному объяснить, то вот так она выводится:
FE * (Pot + Bet) + (1 - FE) * EQ * (Pot + Bet + Call) - Bet = 0
FE * (Pot + Bet) + EQ * (Pot + Bet + Call) - FE * EQ * (Pot + Bet + Call) - Bet = 0
FE * (Pot + Bet) - FE * EQ * (Pot + Bet + Call) = Push - EQ * (Pot + Bet + Call)
FE * (Pot + Bet - EQ * (Pot + Bet + Call)) = Bet - EQ * (Pot + Bet + Call)
FE = (Bet - EQ * (Pot + Bet + Call)) / (Pot + Bet - EQ * (Pot + Bet + Call))
Из первой формулы можно вывести и минимальное необходимое эквити, при заданном количестве фолда. Мы просто EQ переносим в одну сторону, а всё остальное в другую:EQ = (Bet - FE * (Pot + Bet)) / ((1 - FE) * (Pot + Bet + Call))
Для нашего случая, скажем, мы знаем, что опп будет фолдить 40%. Подставляем в формулу:
EQ = (10 - 40% * (10 + 10)) / (60% * (10 + 10 + 10)) = 11% - столько эквити нам нужно минимум, чтобы полублеф стал прибыльным
Вот ещё небольшая табличка, сколько нужно фолдов в зависимости от ставки и количества аутов нашего полублефа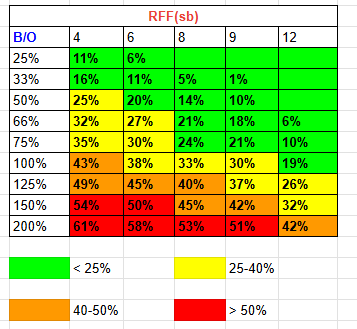
-
Valmiki @ 22.02.25
Необходимая частота фолда для рук с нулевым эквити находится по формуле - риск / (риск + вознаграждение)
То есть, например, ставка 10 bb - это риск, пот 10 bb - вознаграждение, получается 10 / (10 + 10) = 50%
Если приравнять пот к единице, то эту формулу можно выразить как bet / (bet + 1), где bet - размер ставкиЕсли мы говорим про руки, у которых есть некоторое эквити, то формула примет следующий вид - (риск - eq * (2 * риск + вознаграждение)) / (риск - eq * (2 * риск + вознаграждение) + вознаграждение). Её можно записать и так - (bet - eq * (2 * bet + 1)) / (bet - eq * (2 * bet + 1) + 1)
Это может казаться запутанным, но на самом деле не особо. Это всё та же первая формула просто из числителя и знаменателя отнимается - eq * (2 * риск + вознаграждение), то есть пот, который образуется после колла ставки, помноженный на эквити. Для нашего примера это - eq * 30. Почему это вычитается? Простое объяснение - тот, кто ставит с полублефом на самом деле вот этой величиной eq * 30 не рискует, это его законная доля пота, которая ему принадлежит по эквити, поэтому он должен вычесть её из риска изначальной формулы - из числителя и знаменателя. Если по сложному объяснить, то вот так она выводится:
FE * (Pot + Bet) + (1 - FE) * EQ * (Pot + Bet + Call) - Bet = 0
FE * (Pot + Bet) + EQ * (Pot + Bet + Call) - FE * EQ * (Pot + Bet + Call) - Bet = 0
FE * (Pot + Bet) - FE * EQ * (Pot + Bet + Call) = Push - EQ * (Pot + Bet + Call)
FE * (Pot + Bet - EQ * (Pot + Bet + Call)) = Bet - EQ * (Pot + Bet + Call)
FE = (Bet - EQ * (Pot + Bet + Call)) / (Pot + Bet - EQ * (Pot + Bet + Call))
Из первой формулы можно вывести и минимальное необходимое эквити, при заданном количестве фолда. Мы просто EQ переносим в одну сторону, а всё остальное в другую:EQ = (Bet - FE * (Pot + Bet)) / ((1 - FE) * (Pot + Bet + Call))
Для нашего случая, скажем, мы знаем, что опп будет фолдить 40%. Подставляем в формулу:
EQ = (10 - 40% * (10 + 10)) / (60% * (10 + 10 + 10)) = 11% - столько эквити нам нужно минимум, чтобы полублеф стал прибыльным
Вот ещё небольшая табличка, сколько нужно фолдов в зависимости от ставки и количества аутов нашего полублефа
Отличная табличка! Она же как я понял в статье с run it once - https://upswingpoker.com/fold-equity/
-
sashen_ka, ага, та же фигня, только там эквити в процентах, а у меня в аутах. За один аут я взял 2,13% эквити.
-
Valmiki, Вау! Это реально сильно.
Почувствовал себя студентом математического вуза, пока в это всё вникал 😄
Формула отличная, нигде такую не видел. Хотя довольно много сайтов русскоязычных пересмотрел по этой теме, что-то нигде не нашёл ничего подобного.
Отдельное спасибо за то, что вывели эту формулу, которая мне и была нужна:
Valmiki @ 22.02.25
EQ = (Bet - FE * (Pot + Bet)) / ((1 - FE) * (Pot + Bet + Call))
И ещё, вот этот момент тяжело понять логически:
(Но в целом, думаю это не обязательно)
Valmiki @ 22.02.25
от, кто ставит с полублефом на самом деле вот этой величиной eq * 30 не рискует, это его законная доля пота, которая ему принадлежит по эквити, поэтому он должен вычесть её из риска изначальной формулы - из числителя и знаменателя.
В общем, огромное спасибо всем за помощь и отдельное Valmiki!
P.S.
Я удивлён, как люди составляют стратегию игры без этих формул.
Например, нужно составить диапазон ставки на полублефе.
Как понять границу ВОЗМОЖНЫХ для ставки рук без данной формулы?
Смотрел много обучающих роликов, там всё как будто на опыте и интуиции сделано, но не на математических вычислениях.
Со ставками на велью - дела получше обстоят, но не часто вижу, чтобы люди пользовались матрицей эквити в ФЗ для расчётов и т.д.
А ведь это по сути - база!
-
Valmiki @ 22.02.25
Необходимая частота фолда для рук с нулевым эквити находится по формуле - риск / (риск + вознаграждение)
То есть, например, ставка 10 bb - это риск, пот 10 bb - вознаграждение, получается 10 / (10 + 10) = 50%
А что если например хиро уже вложил некоторое количество денег в пот?
Я к тому что необходимо учитывать еще и те финансы которые вложил сам хиро в пот,ведь в случае выигрыша он их себе просто вернет, а не получит прибыль
Пример:У хиро против оппа 0 процентов эквити
Хиро может выиграть только блефом
Нужно рассчитать количество фолдов оппа чтобы ЧИСТЫЙ блеф против него был прибыльным
Возьмем формулу:СВВХДП/Пот=Процент фолдов оппа.
СВВХДП - Сумма Всех Вложенных Хиро Денег в Пот(то есть опен-рейз,колл,рейз,ре-рейз и прочее)Ситуация 1:
Префлоп:
Хиро опен рейз 50бб и опп колл
Пот 100бб
Флоп/терн чек-чекРивер:
Хиро рейз 100бб в банк 100бб и банк становиться 200бб(так как после рейза хиро 100бб,обратно он их вернуть уже не сможет,а значит они уже вложены в пот)Опп пока что вложил в банк только 50бб(колл опен-рейза) а хиро вложил уже 150бб(опен рейз 50бб плюс рейз на ривере 100бб)
Подставляем значения в формулу и получаем 150/200=75 процентов фолдов нужно от оппа
Значит:
25%*(-150) = - 3750 в случае колла оппа75%*(+50) =3750 в случае фолда оппа
Итого матожидание равно 0
Ситуация 2:Префлоп:
Хиро опен рейз 160бб и опп колл
Пот 320бб
Флоп/терн чек-чекРивер:
Хиро рейз 80бб в банк 320бб и банк становиться 400бб(так как после рейза хиро 80бб,обратно он их вернуть уже не сможет,а значит они уже вложены в пот)Опп пока что вложил в банк только 160бб(колл опен-рейза) а хиро вложил уже 240бб(опен рейз 160бб плюс рейз на ривере 80бб)
Подставляем значения в формулу и получаем 240/400=60 процентов фолдов нужно от оппа
Проверяем:
40%*(-240) = - 9600 в случае колла оппа60%*(+160) =9600 в случае фолда оппа
Итого матожидание равно 0
-
Fawn @ 22.02.25
Формула отличная, нигде такую не видел. Хотя довольно много сайтов русскоязычных пересмотрел по этой теме, что-то нигде не нашёл ничего подобного.
Существует довольно прочная традиция считать EV по методу вин-луз относительно текущего банка, типа - (%W * $W) – (%L * $L), где $W - это текущий банк (10 bb), если опп сбросит, или текущий банк + ставка (20 bb), если он заколлит, а $L - наша ставка. Да, она более распространена, по привычке с мохнатых годов или в таком формате проще воспринимать, не знаю. Но есть и другие способы. То, что я использовал, - это эквити * выигрыш - инвестиция, где инвестиция - по-прежнему наша ставка, но мы как бы исходим из того, что всегда её теряем, а выигрыш соответственно здесь - это уже та сумма, которая перемещается к нам из банка напрямую, уже по факту, то есть то, что нам возвращается: когда мы заставим оппонента сбросится (20 bb) или когда выиграем на вскрытии (30 bb). Это та же самая фигня, только меньше переменных, лично мне она больше нравится.
Fawn @ 22.02.25
И ещё, вот этот момент тяжело понять логически
Наше эквити будет иметь значение только тогда, когда нас уравняют. В этом случае банк будет равен 30 бобам. Мы можем считать, что фишки всегда поедут к нам, когда мы доезжаем, то есть eq раз. То есть мы всегда можем рассчитывать на 30*eq бб, в случае колла. Рекурсия какая-то, но, да, получается, мы не рискуем ими.
Elijah96 @ 22.02.25
А что если например хиро уже вложил некоторое количество денег в пот?
Он определённо вложил деньги в пот, иначе бы он до этого спота не добрался. Только эти деньги уже мёртвые. В данном случае мы считаем ЕВ не всей раздачи, а конкретной точки принятия решения. И в этой точке ЕВ фолда равно нулю. То есть мы определяем прибыльность конкретного действия, не набора действий, начиная с префлопа. Да, можно взять за исходную точку что-то другое и посчитать EV какой-то линии, протянувшейся на несколько улиц, но в конкретном случае это не нужно.
-
Valmiki @ 22.02.25
Он определённо вложил деньги в пот, иначе бы он до этого спота не добрался. Только эти деньги уже мёртвые. В данном случае мы считаем ЕВ не всей раздачи, а конкретной точки принятия решения. И в этой точке ЕВ фолда равно нулю. То есть мы определяем прибыльность конкретного действия, не набора действий, начиная с префлопа. Да, можно взять за исходную точку что-то другое и посчитать EV какой-то линии, протянувшейся на несколько улиц, но в конкретном случае это не нужно.
То есть по формуле риск / (риск + вознаграждение) считается не чистая прибыль,а прибыльно ли действие вообще?
Например хиро уже вложил деньги в пот скажем на префлопе,флопе и терне,а на ривере он решил посчитать фолд эквити по этой риск / (риск + вознаграждение) формуле.
Тогда расчеты покажут прибыльно ли действие а не саму прибыль?Я имею ввиду что помимо хиро в пот вложили деньги и другие игроки,и в случае фолда онных,хиро заберет свои ранее вложенные деньги,а так же деньги и других игроков,тем самым получив прибыль,так?
Valmiki @ 22.02.25
И в этой точке ЕВ фолда равно нулю.
ЕВ фолда или просто ЕВ в данной точке?
Сообщение отредактировал Elijah96 - 22.2.2025, 22:31 -
А эта формула FE = (Bet - EQ * (Pot + Bet + Call)) / (Pot + Bet - EQ * (Pot + Bet + Call)) фолд эквити с учетом эквити руки?
-
Elijah96, а зачем нам считать прибыль всей раздачи? Приведу аналогию. Допустим, мы играем в монетку. Игра состоит из 10 подбрасываний. Перед каждым подбрасыванием оппонент предлагает условия по типу: "мои два доллара против твоего одного, что выпадет орёл", а мы либо соглашаемся, либо нет. Если соглашаемся, оба игрока складывают деньги в банк, монетка бросается, если побеждаем, банк наш. Чтобы принимать максимально выгодные решения на протяжении всей игры, нам не нужно считать ожидание всего матча, не нужно учитывать предыдущие и будущие решения, нам достаточно посчитать EV этого конкретного отдельного подбрасывания, которое нам предлагают. Если мы заколлируем, это принесёт нам прибыль в размере 3*0.5-1=0.5 долларов на дистанции. Сфолдим - это ничего нам не принесёт. 0.5>0. Изи колл. Это конкретное решение будет выгоднее. Нам не нужно вспоминать, как мы играли раннее, чтобы выбрать верное решение. То же самое и в покере. Мы можем рассматривать каждый отдельный раунд торговли как отдельное подбрасывание. Тогда деньги в банке считаются мёртвыми. ЕВ фолда всегда равно нулю.
Elijah96 @ 22.02.25
А эта формула FE = (Bet - EQ * (Pot + Bet + Call)) / (Pot + Bet - EQ * (Pot + Bet + Call)) фолд эквити с учетом эквити руки?
Возможно, я не правильно понял вопрос. Но тут фолд эквити - это просто частота фолда. Почему-то так повелось в покерном коммьюнити называть её фолд эквити, тоже не знаю. Но это повсеместная практика - все так называют частоту фолда. Хотя изначально, насколько я помню, этот термин значил другое - эквити оппонента, которое мы как бы присваиваем, когда он фолдит небезнадёжные руки
-
-
Elijah96 @ 23.02.25
Valmiki, А есть ли тогда формула обратная этой?
Тут считается минимальное эквити с учетом фолд эквити
А есть ли тогда формула для рассчета минимального фолд эквити с учетом эквити?
Вот формула подсчёта ЕВ - FE * (Pot + Bet) + (1 - FE) * EQ * (Pot + Bet + Call) - Bet. Она приравнивается к нулю, так как нас интересует граница, после которой полублеф становится прибыльным. Из неё выводится то, что конкретно интересует, с помощью обычных математических манипуляций:
Если минимальное эквити при заданном количестве фолдов, то вот - EQ = (Bet - FE * (Pot + Bet)) / ((1 - FE) * (Pot + Bet + Call))Если минимально необходимое количество фолдов при заданном эквити, получается такое - FE = (Bet - EQ * (Pot + Bet + Call)) / (Pot + Bet - EQ * (Pot + Bet + Call))
Ну и табличка как раз эту нижнюю границу фолдов и показывает. Тут я уже повторяюсь. Соррян, если чего-то не понимаю.
- Вы сможете оставлять комментарии, оценивать посты, участвовать в дискуссиях и повышать свой уровень игры.
- Если вы предпочитаете четырехцветную колоду и хотите отключить анимацию аватаров, эти возможности будут в настройках профиля.
- Вам станут доступны закладки, бекинг и другие удобные инструменты сайта.
- На каждой странице будет видно, где появились новые посты и комментарии.
- Если вы зарегистрированы в покер-румах через GipsyTeam, вы получите статистику рейка, бонусные очки для покупок в магазине, эксклюзивные акции и расширенную поддержку.

Ку. Тренера, реги, акулы, помогите!
Очень нужна ваша помощь, не могу разобраться с математикой полублефов!
Введение:
Чтобы сделать ставку на велью в покере - мы должны иметь более 50% эквити против диапазона продолжения оппа.
Например, на скриншоте ниже, мы можем ставить на велью только T8's, 66 и 77 :
Я работаю в FlopZilla и легко могу определить, какие руки я могу ставить на велью против конкретного диапазона продолжения.
Совсем иная ситуация с полублефами.
Полублефы:
Я знаю, что такое Реальное ФЭ (фолд эквити) и Требуемое ФЭ.
Если Реальное ФЭ > Требуемого ФЭ = ставка в блеф будет плюсовой, даже с рукой без эквити и принесёт незначительную авто-прибыль.
---
Но что делать, если Реальное ФЭ = Требуемое ФЭ? Или Реальное ФЭ < Требуемое ФЭ?
Как рассчитать, сколько минимально эквити должна иметь рука, чтобы ставить с ней на полублефе при РАЗНОМ количестве ФЭ?
Пример:
Мы хотим поставить пот-бет (100% пота) против оппа, который фолдит на пот-бет РОВНО 40% рук.
Точка безубыточности при ставке в 100% банка = 50%. (Т.е. если опп будет фолдить более 50% рук из своего диапа - ставка в пот будет приносить незначительную автоприбыль.)
Получается, в нашей ситуации Реальное ФЭ < Требуемого ФЭ.
Вопрос: Как рассчитать минимально необходимое эквити руки для ставки на полублефе в такой ситуации?
Буду рад ЛЮБОЙ помощи!
Даже если вы не знаете ответ - ваши рассуждения могут привести к истине. Или, может вы где-то видели материал по этой теме?
Спасибо всем, кто решит поучаствовать!
P.S.
Есть ещё интересная формула:
EV = (Реальное ФЕ - Требуемое ФЕ) + (Эквити руки * реализация эквити)
Но не могу понять, может ли эта формула как-то помочь.