математика расчетов
Статистика
Статистика темы
-
ПопулярностьТоп-3310
-
Постов19
-
Просмотров2,895
-
Подписок1
-
Карма автора0
Лучшие посты автора
Лучшие посты читателей
-
50/50. Либо будет - либо нет
+6
-
не в ту сторону копаешь
+5
-
Где-то у тебя ошибка в рассуждениях, шансы у всех должны быть одинаковы, т.к. события независимы. Эт
0
-
Хоть тебя тут давно не было, я все таки отвечу (может кому-то пригодится). Дальше много букф и цифер
0
-
ауты считать - давео прошлая тема - продвинутая братва считает по-другому - у них есть блокеры. Блок
0
-
-
не в ту сторону копаешь
-
-
закладываешь диапазоны опонентов, смотришь по кол-ву комбинаций как часто будет Ах
-
Poker159 @ 2.5.2013
закладываешь диапазоны опонентов, смотришь по кол-ву комбинаций как часто будет Ах
не о том. не под оппонента.голая математика нужна.
как посчитать в % вероятность наличия А у оппа(префлоп) на btn,если у меня А на со (или ЕР,МР-не важно)?
как посчитать в % вероятность А у btn и sb(одновременно) ,если у меня А на со? -
Я попытался сходу, но запутался. Объясни зачем это нужно, может тогда у энтузиастов интерес и появится?
-
-
на какой улице? ну пусть префлоп. ты видишь 2 своих карты. осталось 50карт и 3 туза.
значит вероятность того, что у btn туз - 2*3/50.
тогда верооятность, что у кого-то(btn sb bb) на этих позицих хотя бы 1 туз - 3*2*3/50.
вроде так. -
1/50+1/49 + 1/48+1/47 + 1/46+1/45 = лень считать
-
topka @ 2.5.2013
значит вероятность того, что у btn туз - 2*3/50.
неправильно.
3/50+47/50*3/49=0,117551
Это независимо от позиции. Ты же так упираешь на то, что ты на СО - очевидно, ты уверен, что если до тебя все выкинули, у них туза гарантированно нет? Это ошибочное допущение. Но если его принять, то для 6-макс, например, получим уже
3/46+43/46*3/45=0,127536Партизан @ 2.5.2013
как посчитать в % вероятность А у btn и sb(одновременно) ,если у меня А на со?
0,117551*0,117551=0,0138
только не стоит рассчитывать, что эти расчеты как-то помогут тебе в игре -
А да, мою формулу на 3 умножить надо. =)
-
Объясни зачем это нужно, может тогда у энтузиастов интерес и появится?
Я учусь играть и считать,поэтому и задал этот вопрос.Стало интересно посчитать вероятность событий.Сам попробывал-запутался.
А вообще, ботоводство - не есть гут.
Не понял о чем ты.
только не стоит рассчитывать, что эти расчеты как-то помогут тебе в игре
Хорошо, не буду.
Asker,спасибо.Спасибо всем. -
-
Партизан @ 1.5.2013
Только учусь.Помогите,пожалуйста,научиться считать вероятности в покере.
Например: на СО у меня Ах. Как рассчитать вероятность в % того,что у кого-то на SB,ВВ,BTN будет тоже Ах ?
С надеждой на понимание.
Гораздо больше помогут знания по подсчету аутов на флопе/терне/ривере и перевод этих аутов в проценты... все просто и полезно, а то что ты хочешь это практически негде применить... -
Партизан @ 1.5.2013
Только учусь.Помогите,пожалуйста,научиться считать вероятности в покере.
Например: на СО у меня Ах. Как рассчитать вероятность в % того,что у кого-то на SB,ВВ,BTN будет тоже Ах ?
С надеждой на понимание.
Изучи сначала таблицу аутов для постфлоп игры , а расчитывать что у когото там что то на ... Лично я думаю что в этом смысла мало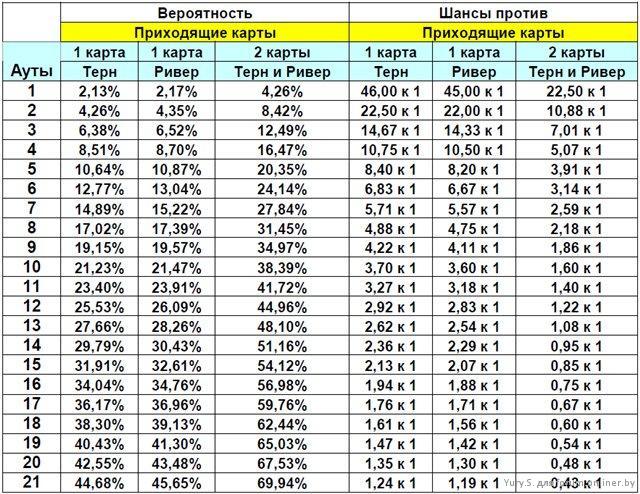
-
лично я считаю только сови ауты. Потом умножаю их на два и получаю свои шансы на победу. Если же дело касается алл-ин, то на флопе при олл-ин нужно свои шансы умножать на 3. Конечно есть погрешность. На флопе 1аут(1/47)=0,021(3), я округлил.Сообщение отредактировал dianacool - 29.5.2013, 0:45
-
dianacool @ 28.5.2013
лично я считаю только сови ауты. Потом умножаю их на два и получаю свои шансы на победу. Если же дело касается алл-ин, то на флопе при олл-ин нужно свои шансы умножать на 3. Конечно есть погрешность. На флопе 1аут(1/47)=0,021(3), я округлил.
ауты считать - давео прошлая тема - продвинутая братва считает по-другому - у них есть блокеры.
Блокеры - это тема. Ей можноправдать все. Например, ты с баттона рейзишь а4 и тебе с сб летит трибет и с бб алын.
Ты пишешь в форум, пацаны, у меня туз, значит у них туза нет все по шансам. Это называется - блокер.
А вот отдельная тема- это когда два туза на флопе. - это из темы блокеров, но гораздо хуже.
Заставляет продавать последнюю одежду участников мультипота .... Ауты - херня. -
Партизан @ 1.5.2013
Только учусь.Помогите,пожалуйста,научиться считать вероятности в покере.
Например: на СО у меня Ах. Как рассчитать вероятность в % того,что у кого-то на SB,ВВ,BTN будет тоже Ах ?
С надеждой на понимание.
Хоть тебя тут давно не было, я все таки отвечу (может кому-то пригодится).
Дальше много букф и цифер :)Если в раздаче изначально вас четверо, а остальные в ситуате, то посчитать можно так:
1 карту раздают SB - его вероятность получить туза - 4/52 = 7,6923%
2 карту раздают BB - его вероятность получить туза: 4/51 (с вероятностью 48/52 [48/52 - вероятность того, что на SB не упал ]) или 3/51 (с вероятностью 4/52), т.е. (4/51)*(48/52)+(3/51)*(4/52)=192/2652+12/2652=204/2652=4/52= 7,6923%
3 карту раздают СО (допустим не туза) принимаем вероятность 100%
4 карту ложат на BTN - его вероятность:
4/49 (с вероятностью (48/52)*(48/52) - вероятность того, что на SB и на ВВ не упал )
или 3/49 (с вероятностью (4/52)*(48/52) - вероятность того, что на SB или на ВВ упал один )
или 2/49 (с вероятностью (4/52)*(4/52) - вероятность того, что и на SB и на ВВ упали по одному ),
т.е. (4/49)* (48/52)*(48/52)+ (3/49)* (4/52)*(48/52)+ (2/49)* (4/52)*(4/52)= Внимание! = 7,4146%
Дальше по аналогии
5 карту сдают SB (в колоде 48 карт)
((8,33%/100)*((100-7,6923)/100)*( (100-7,6923)/100)*( (100-7,4146)/100))*100=6,5714% если никому не выпал, где 8,33%=(4/48)*100%
Или [(6,25%/100)*(7,6923/100)*( (100-7,6923)/100)*( (100-7,4146)/100)]*100=0,4109% - если выпал кому-то одному, где 6,25%=(3/48)*100%
Или [(4,17%/100)*(7,6923/100)*( 7,6923/100)*( (100-7,4146)/100)]*100=0.0228%- если выпал двоим, где 4,17%=(2/48)*100%
Или 0% если выпало 3 туза, принимаю - так как четвертый туз пойдет на СО
Общая вероятность выпадения туза для 5-й карты 6,5714+0,4109+0,0228=7,0051%
Общая вероятность выпадения туза на SB 7.0051%+7.6923=14.6974%
Чем дальше, тем формула удлиняется, но я думаю, что я ответил на вопрос «Как рассчитать вероятности».
П.С. Методика расчета для меня уникальна, я ее нигде не встречал ни в книгах ни в интернете, а те программы которые видел, считают немного по-другому. Просто как-то сам подумал… по теории вероятности должно быть так.
П.П.С Писал расчет без повторной проверки, поэтому могут быть мелкие ошибки или недочеты.
П.П.П.С. Если такая щепетильная точность не нужна, то считаем просто: ( (3 оставшихся туза в колоде*6 розданных карт оппам)/50 оставшихся карт в колоде)*100%=36% - вероятность того, что у кого-то из оппов есть туз. Или по 12% для каждого оппонента. -
Спасибо,Владимир.
-
TypuPypu @ 30.5.2013
Хоть тебя тут давно не было, я все таки отвечу (может кому-то пригодится).
Дальше много букф и цифер :)Если в раздаче изначально вас четверо, а остальные в ситуате, то посчитать можно так:
1 карту раздают SB - его вероятность получить туза - 4/52 = 7,6923%
2 карту раздают BB - его вероятность получить туза: 4/51 (с вероятностью 48/52 [48/52 - вероятность того, что на SB не упал ]) или 3/51 (с вероятностью 4/52), т.е. (4/51)*(48/52)+(3/51)*(4/52)=192/2652+12/2652=204/2652=4/52= 7,6923%
3 карту раздают СО (допустим не туза) принимаем вероятность 100%
4 карту ложат на BTN - его вероятность:
4/49 (с вероятностью (48/52)*(48/52) - вероятность того, что на SB и на ВВ не упал )
или 3/49 (с вероятностью (4/52)*(48/52) - вероятность того, что на SB или на ВВ упал один )
или 2/49 (с вероятностью (4/52)*(4/52) - вероятность того, что и на SB и на ВВ упали по одному ),
т.е. (4/49)* (48/52)*(48/52)+ (3/49)* (4/52)*(48/52)+ (2/49)* (4/52)*(4/52)= Внимание! = 7,4146%
Дальше по аналогии
5 карту сдают SB (в колоде 48 карт)
((8,33%/100)*((100-7,6923)/100)*( (100-7,6923)/100)*( (100-7,4146)/100))*100=6,5714% если никому не выпал, где 8,33%=(4/48)*100%
Или [(6,25%/100)*(7,6923/100)*( (100-7,6923)/100)*( (100-7,4146)/100)]*100=0,4109% - если выпал кому-то одному, где 6,25%=(3/48)*100%
Или [(4,17%/100)*(7,6923/100)*( 7,6923/100)*( (100-7,4146)/100)]*100=0.0228%- если выпал двоим, где 4,17%=(2/48)*100%
Или 0% если выпало 3 туза, принимаю - так как четвертый туз пойдет на СО
Общая вероятность выпадения туза для 5-й карты 6,5714+0,4109+0,0228=7,0051%
Общая вероятность выпадения туза на SB 7.0051%+7.6923=14.6974%
Чем дальше, тем формула удлиняется, но я думаю, что я ответил на вопрос «Как рассчитать вероятности».
П.С. Методика расчета для меня уникальна, я ее нигде не встречал ни в книгах ни в интернете, а те программы которые видел, считают немного по-другому. Просто как-то сам подумал… по теории вероятности должно быть так.
П.П.С Писал расчет без повторной проверки, поэтому могут быть мелкие ошибки или недочеты.
П.П.П.С. Если такая щепетильная точность не нужна, то считаем просто: ( (3 оставшихся туза в колоде*6 розданных карт оппам)/50 оставшихся карт в колоде)*100%=36% - вероятность того, что у кого-то из оппов есть туз. Или по 12% для каждого оппонента.
Где-то у тебя ошибка в рассуждениях, шансы у всех должны быть одинаковы, т.к. события независимы.
Это как в задаче: есть несколько человек, пусть N. Вытягиваем короткую спичку (она одна в руке у раздающего). Вопрос: каким по очереди лучше вытягивать? У кого шансы лучше/хуже? Первого, последнего, в середине?
Вариантов два: в первом НАДО ее вытащить - это приз! во втором НЕ НАДО ее вытаскивать - тот пойдет за пивом.
Ответ:У всех шансы одинаковы и равны 1/N
Мне кажется проще посчитать так:
Всего пар 1326. Из них пар с 1 тузом точно = 4*48=192 / 1326 = 14,479%, если нужны шансы, что "хотя бы один туз", прибавим еще 6 пар, итого 192+6=198 / 1326 = 14,932% - кому-нибудь придет хотя бы один туз (или два). Точней, не кому-нибудь, а шансы каждого на хотя бы 1 туз в руках.
19 постов
Подписаться на обновления темы по почте
1 человек читает эту тему (1 гость):
Зачем регистрироваться на GipsyTeam?
- Вы сможете оставлять комментарии, оценивать посты, участвовать в дискуссиях и повышать свой уровень игры.
- Если вы предпочитаете четырехцветную колоду и хотите отключить анимацию аватаров, эти возможности будут в настройках профиля.
- Вам станут доступны закладки, бекинг и другие удобные инструменты сайта.
- На каждой странице будет видно, где появились новые посты и комментарии.
- Если вы зарегистрированы в покер-румах через GipsyTeam, вы получите статистику рейка, бонусные очки для покупок в магазине, эксклюзивные акции и расширенную поддержку.

Например: на СО у меня Ах. Как рассчитать вероятность в % того,что у кого-то на SB,ВВ,BTN будет тоже Ах ?
С надеждой на понимание.