Poker & Economics
Статистика
Статистика темы
-
ПопулярностьТоп-1083
-
Постов636
-
Просмотров74,041
-
Подписок54
-
Карма автора+908
Лучшие посты автора
Лучшие посты читателей
-
Ты там не слишком задержался в Воронеже-то?
+5
-
показывать надо всегда только с чёткой и понятной целью. Если чётко не понимаешь, что конкретно ты х
+5
-
учись не делать сам работу, которую должен сделать твой подчинённый, даже если ты видишь, что он дел
+4
-
Типичный пример народного мышления. То есть примеры тысяч и десятков тысяч человек столкнувшихся с п
+4
-
парни, это покерный форум все же)
+4
-
-
Теорема Цермело
В теории игр существует такая теорема. Она говорит о следующем. Пусть есть некоторая конечная игра двух лиц с совершенной информацией (то есть покер не прокатит :)). И пусть есть некоторое подмножество Т ее конечных исходов. Тогда либо игрок 1 может обеспечить исход из Т, либо игрок 2 может обеспечить исход не из Т.
Что это означает?
Давайте возьмем простой пример. Допустим, возможных исхода игры два: победа игрока 1 или игрока 2 (без ничьей). Тогда в качестве подмножества Т можно выбрать, например, победу игрока 1. Теорема утверждает, что либо игрок 1 может обеспечить себе победу, либо игрок 2 может обеспечить победу себе. Просто, не правда ли?
Но действительно ли вы понимаете, что это означает? Есть вагон игр с совершенной информацией, где невозможна ничья. Эти игры как правило связаны с каким-либо стратегическим расставлением фишек (например, Hex). Эти игры больше не имеют смысла. В каждой из этих игр один из игроков может со 100% вероятностью обеспечить себе победу, играя по правильной стратегии.
Что это означает для игр с возможностью ничьей? Это означает, что либо один игрок может обеспечить себе победу, либо другой может обеспечить себе как минимум ничью. Иными словами, для каждой игры возможны два варианта: или в ней выигрывает всегда один игрок (играя правильную стратегию), или в ней всегда будет ничья (опять же, если игроки правильно играют). Разве это не поразительно?
В 2007 году это было продемонстрировано для шашек. Вас кто-то обыгрывал в шашки? Забудьте об этом. Получена абсолютно правильная стратегия для шашек. Компьютер, играя в шашки, больше ничего не просчитывает - он просто знает алгоритм победы. Играя по этой стратегии, вы обеспечите себе минимум ничью (а иногда и победу, если соперник не знаком с этой стратегией). Ее можно найти, например, тут: http://webdocs.cs.ualberta.ca/~chinook/
Для шахмат пока такая стратегия не получена. Теоретически, это возможно - но пока, как я понимаю, не хватает мощностей для ее просчета. Поэтому играющие в шахматы компьютеры пока что "думают", а не "знают". Но надолго ли это? :) -
Поведенческая экономика: эффект якоря
Одна из причин, по которой мне так нравится микроэкономика - её близость к реальности и непосредственно ко мне. В этой науке речь идет о поведении, мотивации, стимулах и т.п. отдельных агентов, то есть, по сути, нас с вами. Все выводы, полученные строго и математически, можно сформулировать словами и примерить на себя: так ли вы себя ведете? Достаточно ли близко описывает модель ваше поведение? Понятно, что сказать подобное про макроэкономику, изучающую, например, поведение государства или ЦБ нельзя :)
В большинстве своем микроэкономика базируется на предположении рациональности агентов. Однако эксперименты показывают, что бывают ситуации, когда агенты не рациональны, когда они ведут себя нестандартно. Приблизительно это изучает поведенческая экономика - наука на стыке микроэкономики и психологии.
Я начну рассказ с формулировки эффекта якоря. Допустим, есть некоторый вопрос (желательно численно сформулированный), о котором у человека нет собственного мнения, знания. Тогда если человеку дать в этот момент некую цифру, то его сознание автоматически "привязывается" к этой цифре (как к якорю), и берет ее за некоторую точку отсчета.
Звучит непонятно и запутанно, но на примерах все гораздо проще. Допустим, вы ловите машину в Москве из центра до Алтуфьево. Вы понятия не имеете о том, сколько это стоит. И вы спрашиваете у водителя: "сколько?". От того, что ответит в этот момент таксист, будет зависеть и ваша оценка. Ваше сознание "привяжется" к этой цифре, и уже не уйдет от нее далеко. Если он скажет "500", то вы подумаете, что наверно справедливая цена около 300, и сторгуетесь на 400. Если он скажет "600", то вы подумаете, что наверно справедливая цена около 400, и сторгуетесь на 500.
"Но это очевидно!" - наверняка скажете вы. В голову сразу приходит простое объяснение - услышав цену таксиста, вы считаете, что она некоторым образом связана с "правильной" ценой, поэтому и ориентируетесь на нее. Это правильное объяснение. Но только частично. И в этом - самая большая удивительность эффекта якоря. Приведу два эксперимента, которые иллюстрируют это.
Эксперимент 1.
В 1974 году Tversky и Kahnemann провели следующий эксперимент. Люди видели, как на колесе фортуны случайным образом выпадает одно из двух чисел: 10 или 65. После этого им задавали два вопроса.
Первый: как вы думаете, процент Африканских стран в ООН больше или меньше выпавшего числа?
Второй: как вы думаете, каков этот процент?
Результаты: среди тех, у кого выпало число 10, средний ответ на 2 вопрос был 25%. Среди тех, у кого выпало 65 - 45.
Поразительно то, что в этом примере якорь был случаен. И люди знали о том, что это просто случайное число - они видели сами, как оно выпало на барабане. Но все равно их сознание привязывалось к нему. Это кардинально отличается от примера с таксистом.
То есть представьте себе: вы собрались продавать машину полному профану. Встречаетесь с ним, и сходу ему: "350". А потом говорите, типа, ой, извините, это я о своем, не о машине. Но уже все - дело сделано. Цена продажи сама повысилась с 310 тысяч до 320 :)
Эксперимент два
2003 год, работа Ariely, Loewenstein, Prelec.
Они взяли случайную выборку людей и предложили им купить разные товары по цене, равной сумме последних двух цифр от их номера социальной страховки. Люди знали, что сумма выбирается таким "случайным" образом. После чего у людей спросили, за какую максимальную цену они бы купили эти товары.
Результаты (картинка в конце поста)
Все участники были разделены на пять групп по возрастанию суммы их последних двух цифр (это отражено в первой колонке). То есть, например, пятая квантиль - это одна пятая всех участников с наибольшими суммами.
Из эксперимента явно видно, что чем больше случайный якорь (сумма последних двух цифр SSN), тем больше сумма, которую люди готовы заплатить за товар.
По-моему, это удивительно. Человек видит выпадение случайного числа, прекрасно осознавая, что оно не имеет никакого отношения к предлагаемому ему товару (выбору, вопросу). Но его сознание, помимо его воли, все равно цепляется за этот якорь и смещает его объективную оценку.
Рассказ базируется на лекциях А. Суворова по поведенческой экономике.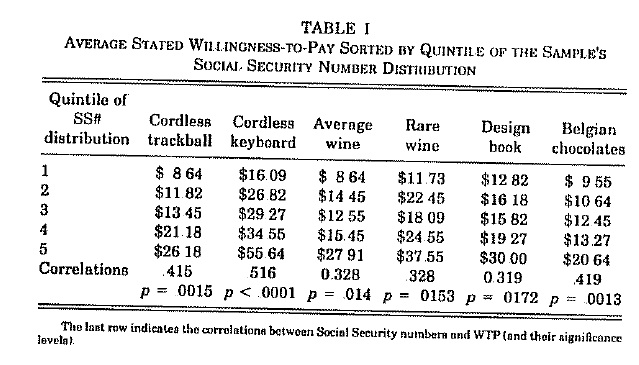
Сообщение отредактировал Maskus - 9.7.2010, 13:16 -
Как по-человечески вставить картинку в середине текста? :)
-
С почином.
Думаю, ожидается интересный дневник -
очень интерестно , только картинку не видно :(
-
Меньше всего я ожидал увидеть тигры в покерном дневнике =))
-
-
Ну картинка сама по себе должна быть немаленького размера, а в качестве сервиса могу порекомендовать savepic.ru - все просто и понятно, можно публиковать картинки без уменьшения.
Надеюсь, интересные темы в дневнике не иссякнут! -
хаюшки
-
Спасибо, очень интересно, пиши еще!
-
якоря это всё из нлп
-
Круто! )
-
Рад видеть, велком)
-
Привет и добро пожаловать!
-
У вас тут аура какая-то особая? :)
Стоило создать блог, как сразу вышел на две финалки. Одну выиграл, на второй вылетел 8м.
-
круто!
-
-
welcome!
интересные статьи, пиши еще -
Как такое возможно? Стать магистром одновременно в двух разных университетах?
Зачем регистрироваться на GipsyTeam?
- Вы сможете оставлять комментарии, оценивать посты, участвовать в дискуссиях и повышать свой уровень игры.
- Если вы предпочитаете четырехцветную колоду и хотите отключить анимацию аватаров, эти возможности будут в настройках профиля.
- Вам станут доступны закладки, бекинг и другие удобные инструменты сайта.
- На каждой странице будет видно, где появились новые посты и комментарии.
- Если вы зарегистрированы в покер-румах через GipsyTeam, вы получите статистику рейка, бонусные очки для покупок в магазине, эксклюзивные акции и расширенную поддержку.

Меня зовут Макс, и я люблю
покерэкономикупокер и экономику.И тем, и другим я увлекаюсь уже около четырех лет и достиг определенных успехов. В покере я играю мтт 50- от себя и 100+ от бэкера. Что касается экономики, то в этом году я закончил два вуза (МФТИ и РЭШ), став магистром экономики и магистром по направлению "прикладные математика и физика", но тоже с уклоном в экономику.
Я буду писать о покере, но буду писать и об экономике. Экономика (прежде всего как наука) для меня - это целый мир, и там полно интересного и захватывающего. Если бы вы только знали, сколько раз я слушал лекции с открытым ртом или по полчаса рассказывал девушке об очередной интересной штуке Больше всего я люблю микроэкономику, финансы и теорию игр.
У меня есть блог на цгм, и посты об экономике из блогов будут пересекаться. Мне просто жутко хочется рассказать об этом как можно большему количеству людей :)
Итак, поехали! :)